前回、Neural Network Console を使用して、ディープラーニングがどういうものかを学びました。
しかし、いざ何かしら有効に使おうと思っても、根本の原理が分かっていないと話にならないと思いました。
そこで今回は、 C++ による実装を通して、 ニューラルネットワークの基本単位である、
パーセプトロンについて学びます。
はじめに
単純パーセプトロンとは、
- 神経細胞(ニューロン)をモデル化したもの
- ニューラルネットワークの基本単位
そして、多層パーセプトロンとは、
- 単純パーセプトロンを複数の層で配置させたニューラルネットワーク
- 入力層、隠れ層、出力層で構成されている
- 入力層:多層パーセプトロンの入力となる層
- 隠れ層:中間層ともいい、入力層と出力層の間に位置する
- 出力層:多層パーセプトロンの出力をする層
となります。
今回はこの多層パーセプトロンを C++ で実装します。
そして、実装した多層パーセプトロンには、排他的論理和を学習させます。
こちらのサイトを参考にさせていただきました。
最終的に構築する多層パーセプトロンのイメージはこんな感じです。
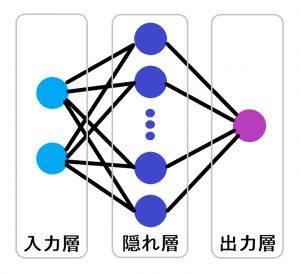
実装
単純パーセプトロン
基本単位である単純パーセプトロンは以下のようになります。ヘッダのみ。
// 単純パーセプトロン
class Perceptron
{
public:
// パーセプトロン間をつなぐためのリンク
struct Link
{
std::weak_ptr<Perceptron> mPerceptron;
double mWeight;
};
public:
Perceptron(const double output = 0.0);
~Perceptron() {}
public:
void Init();
void Init(const std::vector<Link> input);
void Forward(const double output) { mOutput = output; }
void Forward();
void Backward(const double diff);
double Output() { return mOutput; }
private:
static constexpr double Eta = 0.1; // 学習率
private:
std::vector<Link> mInput;
double mOutput;
private:
// シグモイド関数
static double Sigmoid(const double x);
static double DSigmoid(const double x);
};
重みの更新処理(Backward)だけは載せておきます。
再帰的に計算できるようにしました。
ただ未だに正しい処理になっているか自信がないです。。
void Perceptron::Backward(const double diff)
{
// 重みの更新
if (mInput.size() > 0)
{
const double sigmoidDiff = DSigmoid(mOutput) * diff;
// バイアスは更新しない
for (uint32_t i = 0; i < mInput.size() - 1; ++i)
{
auto& link = mInput[i];
link.mWeight -= Eta * link.mPerceptron.lock()->Output() * sigmoidDiff;
const double nextDiff = sigmoidDiff * link.mWeight;
link.mPerceptron.lock()->Backward(nextDiff);
}
}
}
多層パーセプトロン
多層パーセプトロンは以下のような実装をしました。ヘッダのみ。
単純パーセプトロンを各層単位で生成、保持してリンクしています。
// 多層パーセプトロン
// 入力層、隠れ層、出力層の3層
class MultilayerPerceptron
{
public:
static constexpr uint32_t InputNum = 2; // 入力数
static constexpr uint32_t OutputNum = 1; // 出力数
public:
MultilayerPerceptron(const uint32_t hiddenNum);
~MultilayerPerceptron() {}
public:
// 学習
void Study(const double in0, const double in1, const double out)
{
Forward(in0, in1);
Backward(out);
}
// 答える
double Answer(const double in0, const double in1)
{
Forward(in0, in1);
return Output();
}
private:
std::vector<std::shared_ptr<Perceptron>> mInputLayer;
std::vector<std::shared_ptr<Perceptron>> mHiddenLayer;
std::vector<std::shared_ptr<Perceptron>> mOutputLayer;
std::vector<std::shared_ptr<Perceptron>> mHiddenBiasPerceptron;
std::vector<std::shared_ptr<Perceptron>> mOutputBiasPerceptron;
private:
void Forward(const double input_0, const double input_1);
void Backward(const double correct);
double Output();
std::vector<std::shared_ptr<Perceptron>> CreateLayer(const uint32_t num);
std::vector<Perceptron::Link> CreateLink(std::vector<std::shared_ptr<Perceptron>> layer);
};
実行処理
実行処理は以下の通り。
void ExecuteMLP()
{
// 学習データ構造体
struct TrainData
{
double mIn[MultilayerPerceptron::InputNum];
double mOut;
};
constexpr uint32_t HiddenNum = 20; // 隠れ層の数
constexpr uint32_t TrainCount = 1000000; // 総学習カウント
constexpr uint32_t AnsCount = 100000; // 学習状況確認タイミング
// XOR(排他的論理和) の学習データ
constexpr TrainData Data[] =
{
{{0,0},0}, // Q:(0,0) A:0
{{1,0},1}, // Q:(1,0) A:1
{{0,1},1}, // Q:(0,1) A:1
{{1,1},0} // Q:(1,1) A:0
};
srand((unsigned)time(nullptr)); // 乱数初期化
MultilayerPerceptron mlp(HiddenNum); // 3層パーセプトロンを生成
for (uint32_t i = 0; i < TrainCount; ++i)
{
// 学習
for (const auto& data : Data)
{
mlp.Study(data.mIn[0], data.mIn[1], data.mOut);
}
// 学習状況確認
if (i % AnsCount == 0)
{
LOG("== 学習 {0} 回 ==", i);
LOG("Q:(0,0) -> A:{0}", mlp.Answer(0, 0));
LOG("Q:(1,0) -> A:{0}", mlp.Answer(1, 0));
LOG("Q:(0,1) -> A:{0}", mlp.Answer(0, 1));
LOG("Q:(1,1) -> A:{0}", mlp.Answer(1, 1));
}
}
// 最終学習成果
LOG("== 学習 {0} 回 ==", TrainCount);
LOG("Q:(0,0) -> A:{0}", mlp.Answer(0, 0));
LOG("Q:(1,0) -> A:{0}", mlp.Answer(1, 0));
LOG("Q:(0,1) -> A:{0}", mlp.Answer(0, 1));
LOG("Q:(1,1) -> A:{0}", mlp.Answer(1, 1));
}
結果
出力結果は以下の通りになりました。
== 学習 0 回 == Q:(0,0) -> A:0.801351 Q:(1,0) -> A:0.895822 Q:(0,1) -> A:0.921081 Q:(1,1) -> A:0.963905 == 学習 100000 回 == Q:(0,0) -> A:0.549088 Q:(1,0) -> A:0.549772 Q:(0,1) -> A:0.556558 Q:(1,1) -> A:0.398647 == 学習 200000 回 == Q:(0,0) -> A:0.142125 Q:(1,0) -> A:0.894853 Q:(0,1) -> A:0.896008 Q:(1,1) -> A:0.0800954 == 学習 300000 回 == Q:(0,0) -> A:0.0716445 Q:(1,0) -> A:0.945058 Q:(0,1) -> A:0.945519 Q:(1,1) -> A:0.0449508 == 学習 400000 回 == Q:(0,0) -> A:0.0512673 Q:(1,0) -> A:0.960116 Q:(0,1) -> A:0.960406 Q:(1,1) -> A:0.0336502 == 学習 500000 回 == Q:(0,0) -> A:0.0412526 Q:(1,0) -> A:0.967637 Q:(0,1) -> A:0.96785 Q:(1,1) -> A:0.027808 == 学習 600000 回 == Q:(0,0) -> A:0.0351568 Q:(1,0) -> A:0.972261 Q:(0,1) -> A:0.97243 Q:(1,1) -> A:0.0241364 == 学習 700000 回 == Q:(0,0) -> A:0.0309929 Q:(1,0) -> A:0.975442 Q:(0,1) -> A:0.975583 Q:(1,1) -> A:0.0215703 == 学習 800000 回 == Q:(0,0) -> A:0.0279359 Q:(1,0) -> A:0.97779 Q:(0,1) -> A:0.977912 Q:(1,1) -> A:0.0196529 == 学習 900000 回 == Q:(0,0) -> A:0.025578 Q:(1,0) -> A:0.979609 Q:(0,1) -> A:0.979716 Q:(1,1) -> A:0.018153 == 学習 1000000 回 == Q:(0,0) -> A:0.0236931 Q:(1,0) -> A:0.981068 Q:(0,1) -> A:0.981164 Q:(1,1) -> A:0.0169398
学習回数が10万回の段階ではさっぱり学習の成果が見えていませんが、20万回あたりからは、ちゃんと正解に寄ってきています。
最終学習回数(100万回)になると、ほぼ正解に近いに値になっているのが分かります。
ちゃんと学習できているようです。
まとめ
分かったこと
ニューラルネットワークにおいての学習とは、パーセプトロン間に関連付けられた重みが決まることをいうようです。この重みの決定が重要そうです。
そして、この重みを決定づけるために活性化関数がかかわってくるということが分かりました。今回は参考サイトにあるシグモイド関数をそのまま使用しています。
反省点
今回、多層パーセプトロンを実装してみて、パーセプトロンについての理解はある程度深まったかと思いますが、重みを決めるための活性化関数については正確な知識を得られたわけではないです。
実際、シグモイド関数の微分における 0.1 をかける処理など、なぜそうしているか理解できていません。
また、実装した多層パーセプトロンは入力数/出力数が固定されていたりで、他の学習に流用する設計にはなっていません。
今後やりたいこと
今回実装した多層パーセプトロンを基に、入力数、出力数、隠れ層の数を可変にできるようにしてみたいです。
また、活性化関数のバリエーションを増やし、学習内容に向いている活性化関数を取り扱えるようにしたいです。(たとえば画像処理向けにカスタムしてモノを見分けるような)
ニューラルネットワーク関連のライブラリなども充実しているようなので、この辺りも触ってみたいです。Python の学習もかねて。