はじめに
こんにちは!エンジニアのゼイシュウです。
これまで、グラフィックスに興味を持っており、あちこちに触れてきましたが、いずれも浅くしか理解していませんでした。
今回の機会を活かして、グラフィックスおよびレンダリングに関連する知識を体系的に理解し、学ぶことを考えています。
そのため、実際に手を動かして、CPUレンダラーを実装してみました。
スクリーンショット
環境設定
Visual Studio
クロスプラットフォームをまず考えずに、ウインドウズPCで普通にVisual Studioを使いました。
まず空c++プロジェクトを作ります。
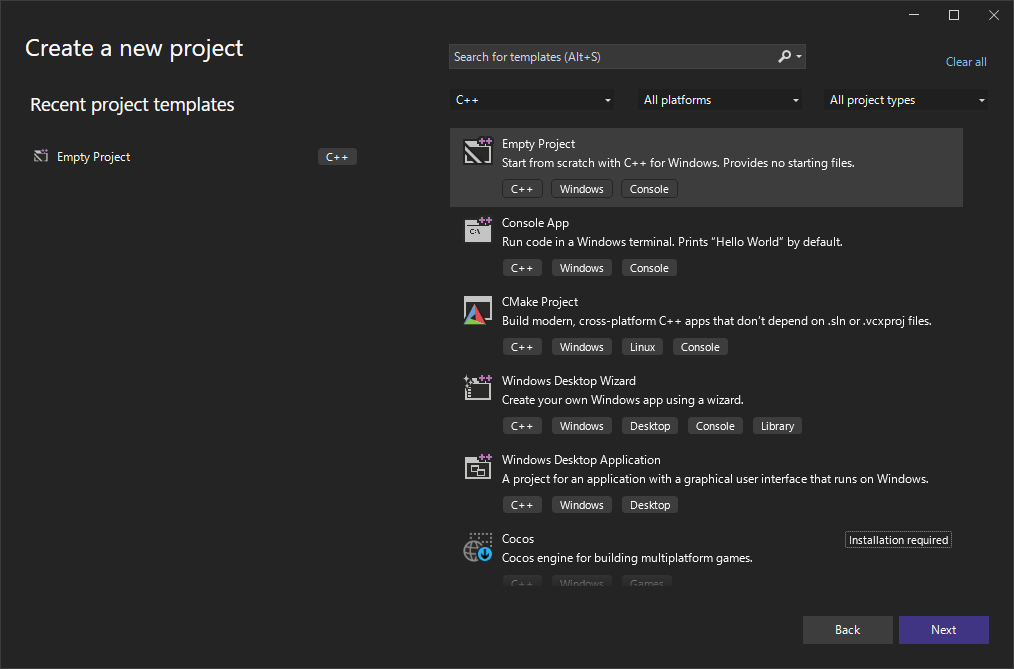
SDL2
SDL2はオーディオ、キーボード、マウス、ジョイスティック、およびグラフィックスハードウェアへのローレベルアクセスを提供するために設計されたクロスプラットフォーム開発ライブラリです。具体的な内容を上記のリンクを確認してください。
今回はカラーバッファをウインドウへ描画する機能だけを使います。
ライブラリーダウンロード
Eigen
あまり複雑な計算がないですが、ベクトルと行列計算数学ライブラリーを使ってみました。
ライブラリーダウンロード
ダウンロードしたライブラリーを解凍し、プロジェクトフォルダーにコピーします。
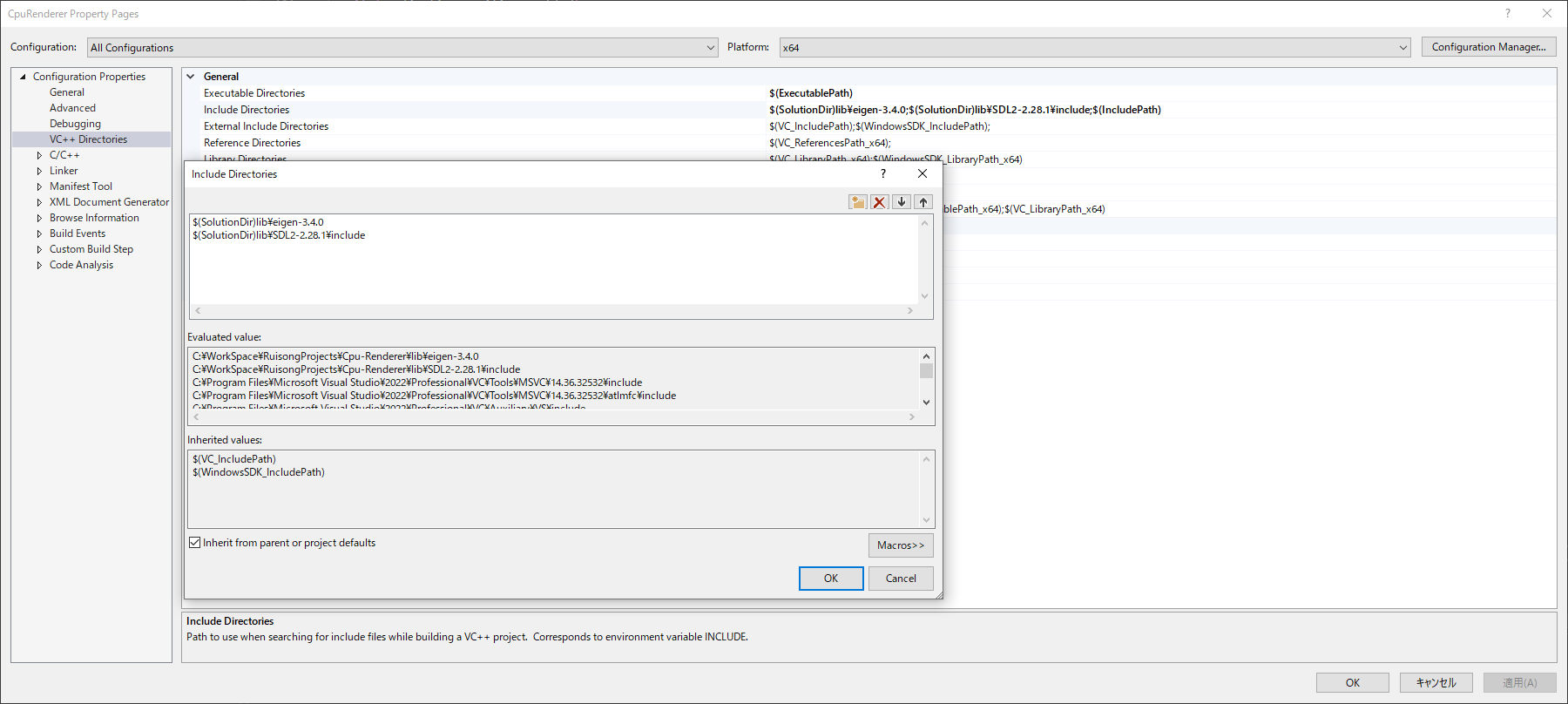
プロジェクトインクルードディレクトリに追加します。
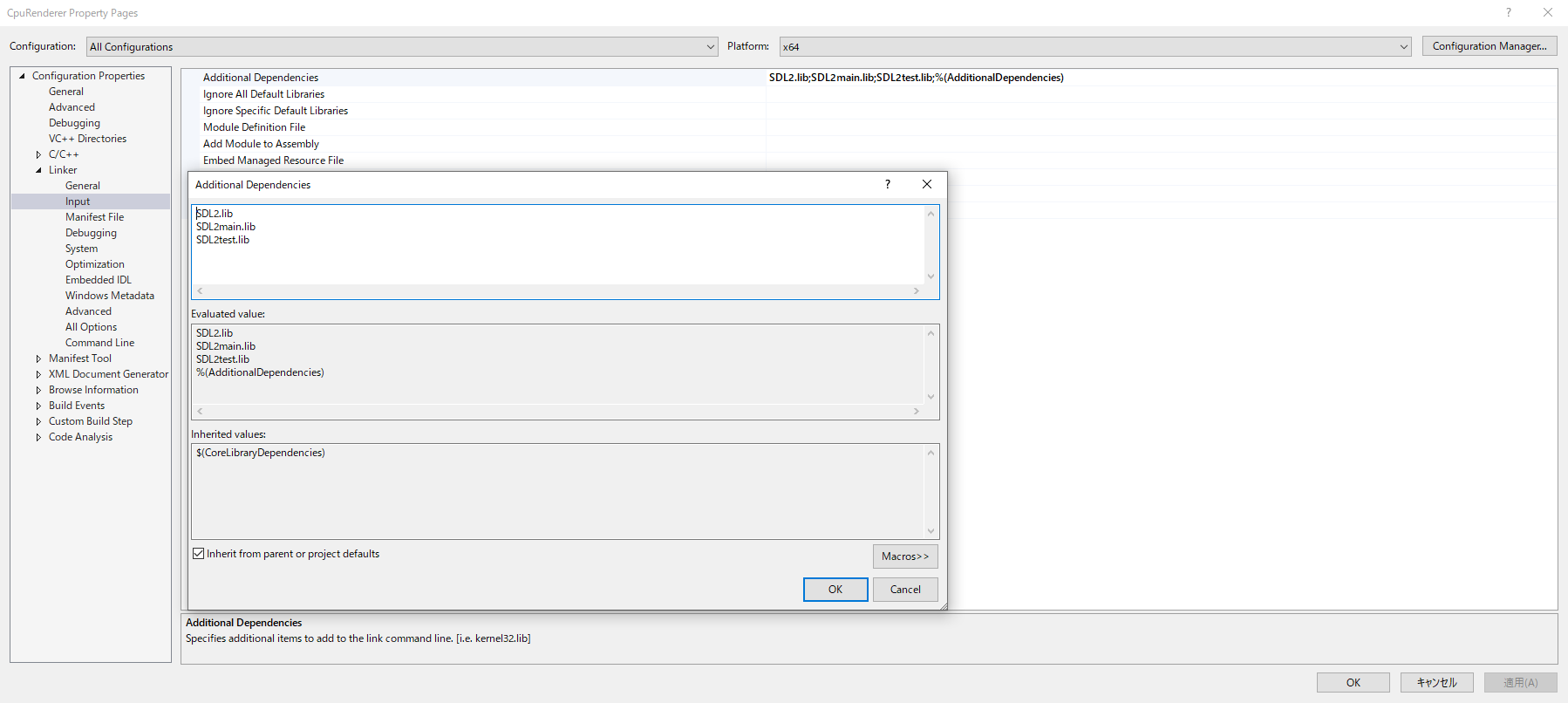
リンカーインプットにLibファイルを追加します。
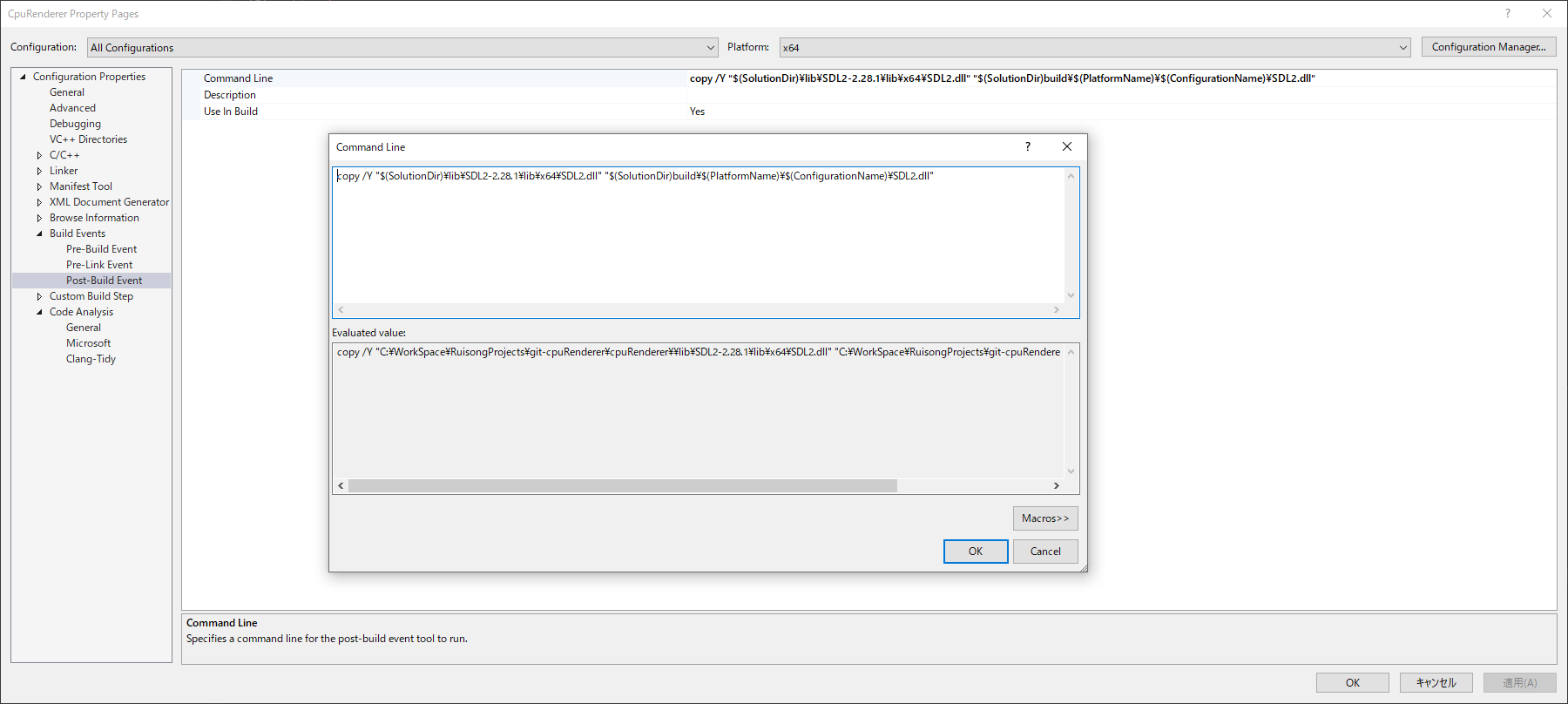
設定の一例として、画像をご参考ください。
そのあと、ポストビルドイベントでSDL.dllを実行フォルダーにコピーするコマンド追加します。
カラーバッファ
SDL2のピクセルデータのデフォルトフォーマットは32ビットですので、
符号なしintの配列をカラーバッファとして使います。
// ウインドウズ設定
class Configuration
{
public:
static constexpr int32_t DisplayWidth = 800;
static constexpr int32_t DisplayHeight = 600;
static constexpr int32_t DisplayPixelCount = DisplayWidth * DisplayHeight;
}
// バッファクラス
template<typename T, size_t Size>
class Buffer
{
public:
std::unique_ptr<std::array<T, Size>> mBuffer;
};
// カラーバッファ
using ColorBuffer = Buffer<uint32_t, Configuration::DisplayPixelCount>;
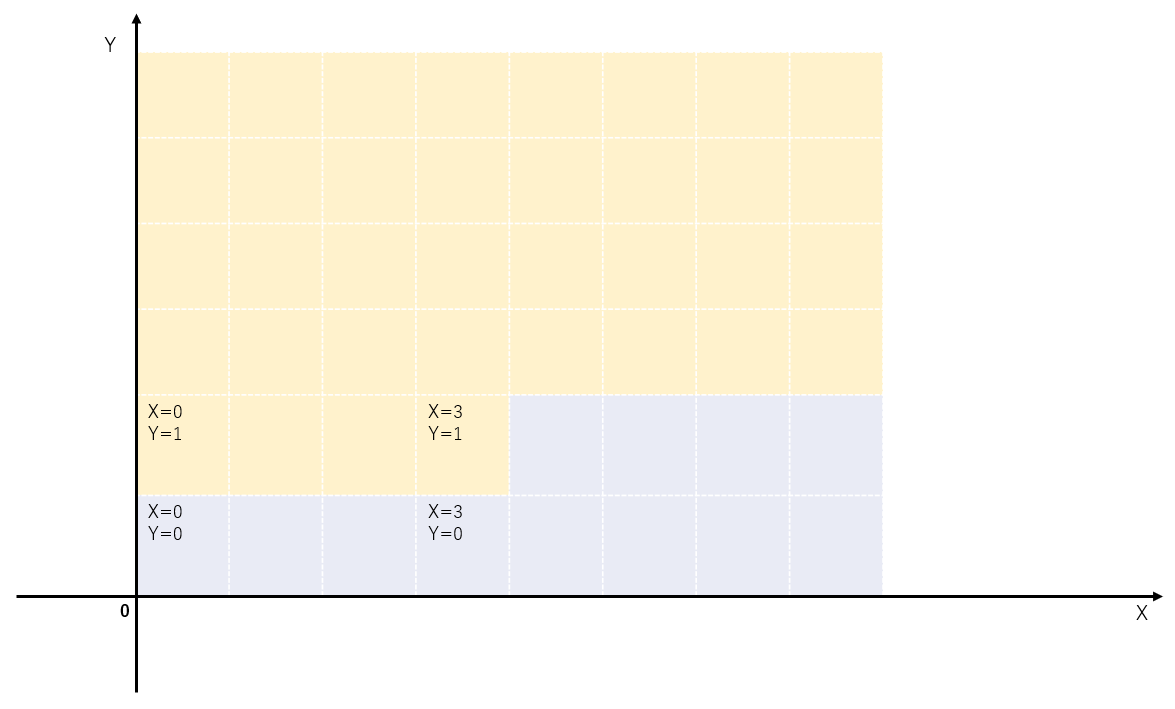
画面座標系の原点は左下隅にありますので、ピクセルの色をxおよびy座標で設定する際、対応するバッファの配列インデックスは (height – y – 1) * width + x です。
template<typename T, size_t Size>
inline void Buffer<T, Size>::SetPixelData(int32_t x, int32_t y, T value)
{
mBuffer->at((mHeight - y - 1) * mWidth + x) = value;
}
キューブデータの準備
今回はカラーキューブですので、頂点データは座標と色データだけで大丈夫です。
// 頂点データ
struct ColorVertex
{
Vec3f mPosition;
Color mColor;
};
普通の24頂点キューブデータを用意します、以下はイメージです。
// キューブインデックスバッファ
std::vector<int32_t> indices =
{
1, 0, 3,
3, 2, 1,
...//省略
};
// キューブ頂点バッファ
std::vector<ColorVertex> vertices =
{
//裏面
ColorVertex{Vec3f(-1.0f, -1.0f, -1.0f), Color::Blue()},
ColorVertex{Vec3f(1.0f, -1.0f, -1.0f), Color::Yellow()},
ColorVertex{Vec3f(1.0f, 1.0f, -1.0f), Color::Red()},
ColorVertex{Vec3f(-1.0f, 1.0f, -1.0f), Color::Green()},
...//省略
};
頂点データのトランスフォーム
頂点データを正確にスクリーン描画するためには、画像のように一連変換を行います。
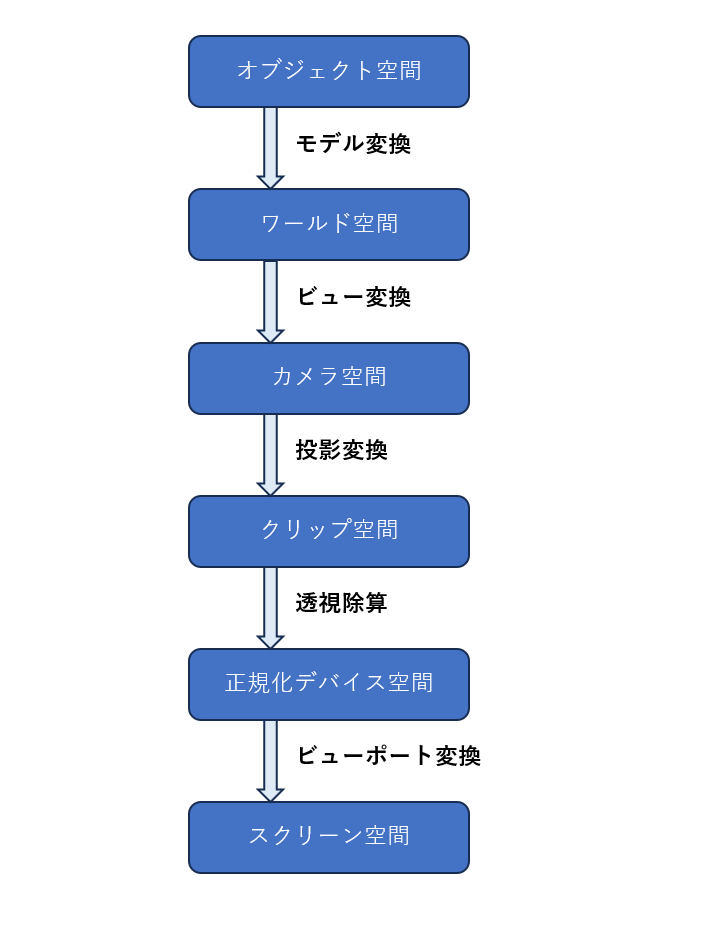
モデル変換
今回のキューブはY軸で回転を行います。
EigenはQuaternionから回転行列変換する関数を用意していますので、Quaternionで回転を表示します。
// EigenのQuaternionfを使う using Quaternion = Eigen::Quaternionf; // Modelクラスメンバー Quaternion mRotation = Quaternion::Identity(); // Y軸を基準として回転 mRotation.w() = std::cos(theta); mRotation.y() = std::sin(theta);
トランスレーションはVec3fで表示します。
そのため、モデル行列の取得は以下となります。
```c++
// Modelクラスのメンバー、トランスレーションを表示する
Vec3f mPosition = Vec3f::Zero();
// モデル行列取得
Mat4f Model::GetModelMatrix()
{
// 回転行列はQuaternionから取得
Mat4f rotationMat = Mat4f::Identity();
rotationMat.block(0, 0, 3, 3) = mRotation.toRotationMatrix();
// トランスレーション行列を作る
Mat4f translateMat = Mat4f::Identity();
translateMat <<
1.0f, 0.0f, 0.0f, mPosition.x(),
0.0f, 1.0f, 0.0f, mPosition.y(),
0.0f, 0.0f, 1.0f, mPosition.z(),
0.0f, 0.0f, 0.0f, 1.0f;
// モデル行列計算、回転を先に行いますので、順番は重要
return translateMat * rotationMat;
}
ビュー変換
ワールド座標系からカメラ座標系に変換するためには、カメラを定義します。
カメラの位置と注視点座標でカメラ向き方向を計算できます。
外積でカメラ左方向、上方向を計算したら、ビュー行列の取得もできました。
具体的な説明はこのリンクを参考してください。
// Cameraクラス定義したメンバー
Vec3f mPosition = Vec3f(0.0f, 3.0f, 8.0f);
Vec3f mTarget = Vec3f::Zero(); // カメラ注視点
Vec3f mUp = Vec3f::UnitY(); // 座標系上方向
// View Matrix計算
Mat4f Camera::GetViewMatrix()
{
// カメラ向き方向
Vec3f forward = mPosition - mTarget;
forward.normalize();
// カメラ左方向
Vec3f left = mUp.cross(forward);
left.normalize();
// カメラ上方向
Vec3f up = forward.cross(left);
// View Matrix
Mat4f viewMat;
viewMat <<
left.x(), left.y(), left.z(), -left.dot(mPosition),
up.x(), up.y(), up.z(), -up.dot(mPosition),
forward.x(), forward.y(), forward.z(), -forward.dot(mPosition),
0, 0, 0, 1;
return viewMat;
}
透視投影変換
次に、投影行列の計算を行います。投影行列の計算においては、カメラの視錐台内の座標をNDC(正規化デバイス座標)にマッピングする必要があります。
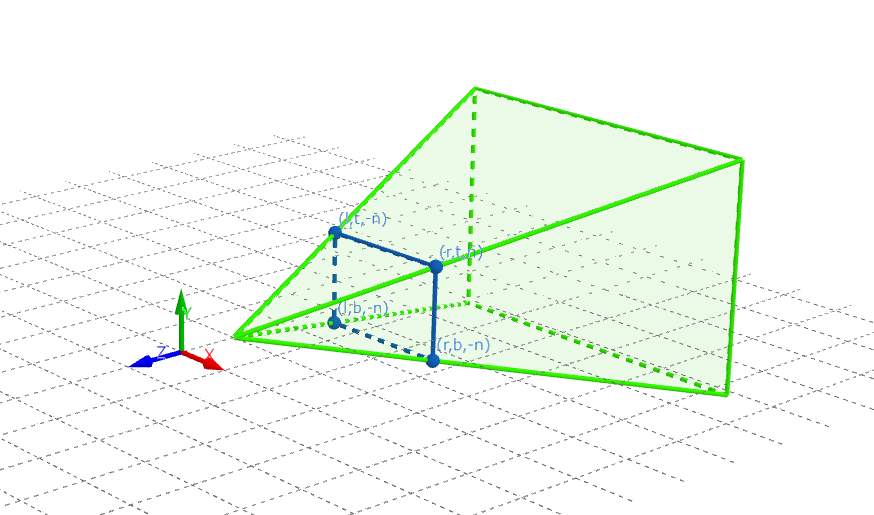
ここで、rは近接平面のx軸正の座標を表し、tは近接平面のy軸正の座標を表します。具体的な説明と計算方法については、このリンクを参照してください。これにより、投影行列を得ることができます。
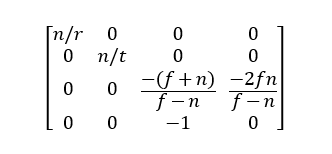
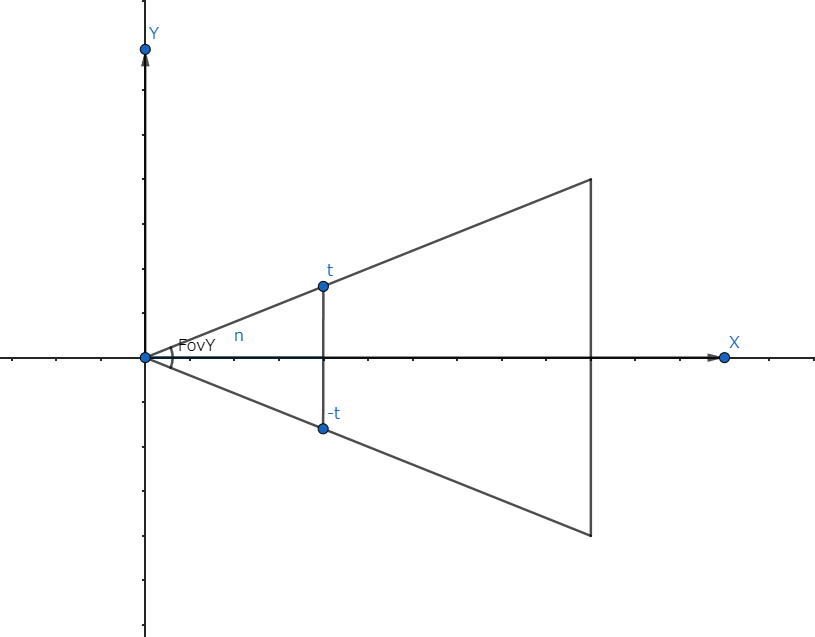
rとtを計算します。上図から以下の式を得ます。

アスペクト比はすでにわかりますので、最後の透視投影行列は以下となります。
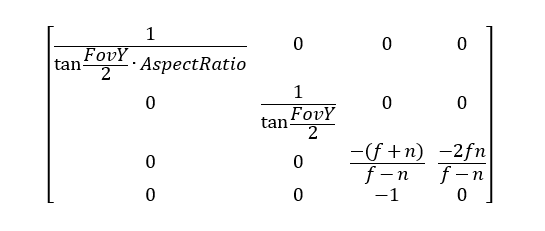
実装は以下となります。
Mat4f Camera::GetPerspProjMatrix()
{
Mat4f perspProjMat;
const auto zRange = mFar - mNear;
const auto mat11 = 1.0f / std::tan(mFovy * 0.5f);
perspProjMat <<
(mat11 / mAspectRatio), 0.0f, 0.0f, 0.0f,
0.0f, mat11, 0.0f, 0.0f,
0.0f, 0.0f, ((-mNear - mFar) / zRange), (-2.0f * mFar * mNear / zRange),
0.0f, 0.0f, -1.0f, 0.0f;
return perspProjMat;
}
正規化デバイス座標計算
MVP変換をした後、正しいNDC座標を取得するために、結果のベクトルをw成分で割る必要があります。
Mat4f mvp = mProjectionMatrix * mViewMatrix * mModelMatrix;
// クリップ空間に変換
std::array<Vec4f, 3> vertices;
for (size_t i = 0; i < 3; i++)
{
const ColorVertex vertexPos = t.at(i).mPosition;
vertices.at(i) = mvp * Vec4f(vertexPos.x(), vertexPos.y(), vertexPos.z(), 1.0f);
}
// NDC座標計算
for (auto& v : vertices)
{
v /= v.w();
}
ビューポート変換
このステップはNDC座標からスクリーン座標に変換します。
具体的な説明をこのリンクを参考してください。
// 入力のNDC座標
std::array<Vec4f, 3> vertices;
// 出力スクリーン座標
std::array<Vec2f, 3> screenCoords;
// 出力深度値
std::array<float, 3> screenDepths = {};
// 三角形各頂点処理
for (size_t i = 0; i < 3; i++)
{
const auto& v = vertices.at(i);
screenCoords.at(i) = Vec2f(
Configuration::DisplayWidth * 0.5f * (v.x() + 1.0f),
Configuration::DisplayHeight * 0.5f * (v.y() + 1.0f));
screenDepths.at(i) = 0.5f * (v.z() + 1.0f);
}
以上でやっとスクリーン座標を得ることができました。
三角形のラスタライズ
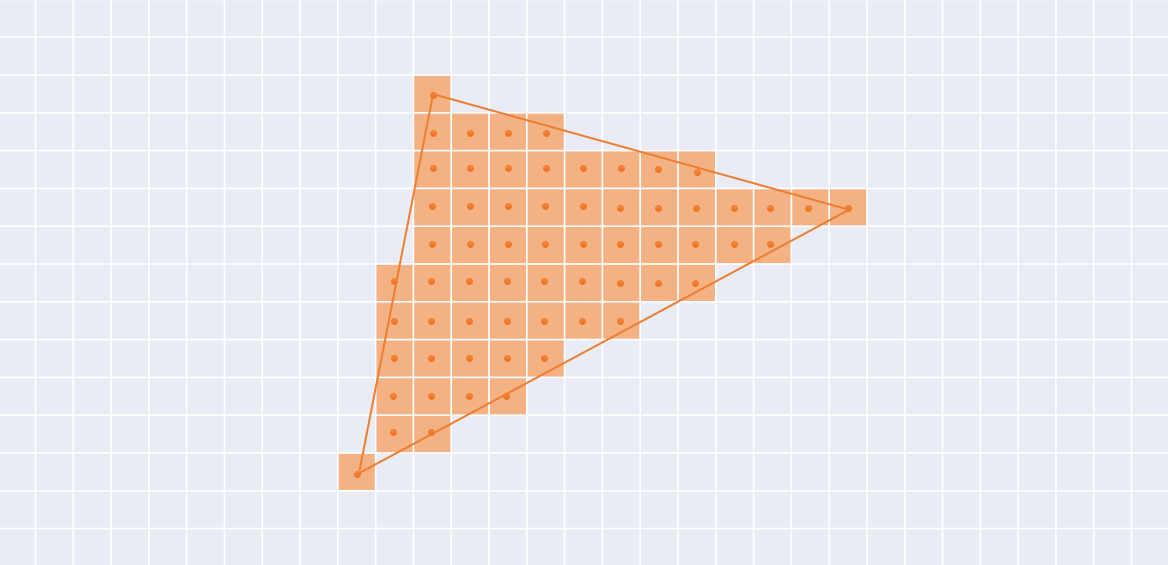
重心座標の3つの成分のうち、どれか1つでも0より小さい場合、そのピクセルは三角形の外部にあり、着色する必要はありません。
深度値を計算して、このピクセル更新かどうかを判断します。
// ボンディングボックス取得
BoundingBox bb = GetTriangleBoundingBox(screenCoords);
for (int32_t x = bb.mMin.x(); x <= bb.mMax.x(); x++)
{
for (int32_t y = bb.mMin.y(); y <= bb.mMax.y(); y++)
{
// ピクセル中心に調整
Vec2f point = Vec2f(0.5f + x, 0.5f + y);
// 重心座標計算
Vec3f weight = CalculateWeight(screenCoords, point);
// 三角形中かどうか判別
if (weight.x() >= 0 && weight.y() >= 0 && weight.z() >= 0)
{
// 深度値補間
float depthInter = DepthInterpolate(screenDepths, weight);
// 色補間
Color colorInter = ColorInterpolate(vertexColor, weight);
// 深度値により、ピクセル色を更新する
if (depthInter < depthBuffer(x, y))
{
depthBuffer.SetPixelData(x, y, depthInter);
colorBuffer.SetPixelData(x, y, colorInter.Data());
}
}
}
}
これまでは色付けキューブを描画するための実装を大まかに書きました。
まとめ
今回のCPUレンダラーの実装で、グラフィックスの知識を勉強と理解ができました。
グラフィックスでまだたくさん勉強したいことがありまして、
シリーズブログになるかもしれません、お楽しみください。
今回実装したリポジトリです。