プログラムをやっていると多角形から情報を取り出すことが必要になることがたまにあります。
過去にそういう状況になった際に使用した計算をいくつかご紹介します。
前提条件
処理をするうえで入力する情報(頂点の情報)に条件を設定しました。
これは目的に応じて処理を簡略化するため行います。
ここでは以下の条件となります。
- 扱うのは2次元の図形
- 多角形である
- 自己交差している図形は入力しない
- 始点と終点は同じ値を入れる
自己交差している図形というのはこういうものです。
四角形なのですが自身の図形の中で交差が存在しています。

不要な点の削除
多角形の頂点としてなくてもいいものを削除します。
そんな点があるのかといいますと見た目上はありません。
ただプログラム的には存在する可能性があります。
例えば(-1,0),(0,0),(1,0)の三角形です。
三角形と言いましたがこれは直線です。
辺の中に頂点がある場合は削除します。
ある頂点の前後の辺の角度が180°の場合に削除するのですがここではほぼ直線のものも直線に補正します。
2辺の成す角を調べるというのは内積を使えばいいですね。
void DeleteRedundantPoint(std::vector<Vector2>& points)
{
std::vector<Vector2> result;
Vector2 a, b;
for (size_t i = 0; i+1 < points.size(); ++i) {
// 最後の要素に始点と同じ点が入っているので始点だけ前の辺をとる方法が違います
if (i == 0) {
a.SetSub(points[points.size() - 2], points[i]);
b.SetSub(points[i + 1], points[i]);
} else {
a.SetSub(points[i - 1], points[i]);
b.SetSub(points[i + 1], points[i]);
}
a.Normalize();
b.Normalize();
// 179°以上はまっすぐにするので追加しません
if (a.Dot(b) > std::cos(PI * (179.0f / 180.0f))) {
result.push_back(points[i]);
}
}
// 始点と終点は同じにします
result.push_back(result[0]);
// pointsに反映
std::swap(points, result);
}
PIは円周率です。
Vector2はこれです。
今後も出てきます。
struct Vector2
{
Vector2() :x(0.0f), y(0.0f) {};
Vector2(float _x, float _y) :x(_x), y(_y){};
float Dot(const Vector2& point) const{
return (x * point.x) + (y * point.y);
}
Vector2& SetSub(const Vector2& a, const Vector2& b) {
x = a.x - b.x;
y = a.y - b.y;
return *this;
}
float Length() const{
return std::sqrt(x*x + y*y);
}
void Normalize(){
float mag = 1.0f / Length();
x *= mag;
y *= mag;
}
float x;
float y;
};
多角形の面積
これで求まります。
float GetArea(const std::vector<Vector2>& points)
{
float result = 0.0f;
for (size_t i = 0; i + 1 < points.size(); ++i) {
result += (points[i].x - points[i+1].x) * (points[i].y + points[i + 1].y);
}
result *= 0.5f;
return result;
}
面積がわかったところでどうなるかというと、これの正負を調べることで入力された図形が右回りか左回りかがわかります。
処理をしていく中でこの方向は一方に統一した方がわかりやすいと思います。
ここでは右回りに統一して処理します。
このGetAreaでは負の値の場合が右回りになっています。
多角形の内外判定
とある点が多角形の内側にあるかどうかを調べます。
その点からみて多角形の各頂点を通って1周したときの角度の和が1周していれば内側です。
bool IsInsidePoint(const std::vector<Vector2>& points, const Vector2& pos)
{
Vector2 a, b;
float angle = 0.0f;
for (size_t i = 0; i + 1 < points.size(); ++i) {
a.SetSub(points[i], pos);
b.SetSub(points[i + 1], pos);
a.Normalize();
b.Normalize();
angle += std::acos(a.Dot(b));
}
return std::fabs(angle) >= 2.0f*PI;
}
大まかに取れればいい場合はこれでよいと思います。
多角形の分割
n角形はn-2個の三角形に分割できます。
分割するには隣り合う頂点と三角形を作るだけ、とはなりません。
凸型であれば問題なのですが凹型ですと図形の外部で三角形ができてしまう場合があります。
凸型多角形とはこのようなものです。
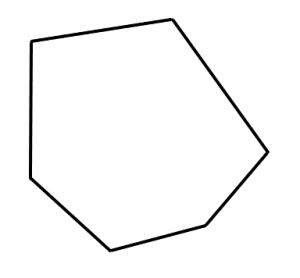
凹型多角形はこれです。へこんでいる部分があります。
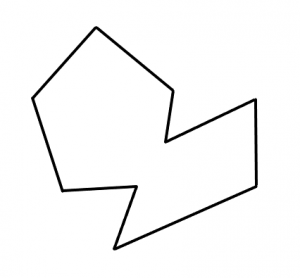
問題となるケース。赤い部分で切り取ってしまうと本来の形になりません。
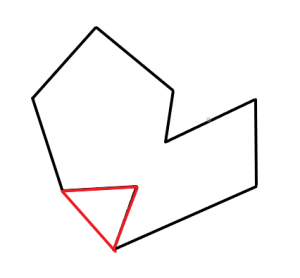
このような形で切り取られることを防ぎます。
切り取った三角形は必ず多角形の内側に存在します。
ですので内側にある場合だけ切り取ればいいのです。
さて、ある辺において内側の方向はどうなるでしょうか。
頂点の並びを右回りに統一しているとありましたね。
ということは右側が内側ということです。
次の頂点への辺の右側に前の頂点があれば切り取ることができます。
少し格好悪い部分もありますがプログラムはこうなります。
void SeparatePoints(const std::vector<Vector2>& in_points, std::vector<Vector2>& out_points)
{
// 削除しながら進めるのでコピーします
std::vector<Vector2> tmp = in_points;
Vector2 a, b;
out_points.clear();
// ここの処理においては最後の要素が始点と同じになっていると不都合なので削除しておきます
tmp.pop_back();
// 最後の3角形になるまで繰り返し
while (tmp.size() > 3) {
std::vector<Vector2>::iterator it = tmp.begin();
// 分割できる三角形を検索します
for (size_t i = 0; i < tmp.size(); ++i) {
// aは前の頂点へのベクトル、bは次の頂点へのベクトルになります
if (i == 0) {
a.SetSub(tmp[tmp.size() - 1], tmp[i]);
b.SetSub(tmp[i + 1], tmp[i]);
} else if (i + 1 == tmp.size()) {
a.SetSub(tmp[i - 1], tmp[i]);
b.SetSub(tmp[0], tmp[i]);
} else {
a.SetSub(tmp[i - 1], tmp[i]);
b.SetSub(tmp[i + 1], tmp[i]);
}
// aの方向がbの内側にあればこの3点はOK
// 頂点の並びを右回りにしていれば内側の方向は以下になります
Vector2 inside_dir(b.y, -b.x);
if (inside_dir.Dot(a) >= 0.0f) {
if (i == 0) {
out_points.push_back(tmp[tmp.size() - 1]);
} else {
out_points.push_back(tmp[i - 1]);
}
out_points.push_back(tmp[i]);
if (i + 1 == tmp.size()) {
out_points.push_back(tmp[0]);
} else {
out_points.push_back(tmp[i + 1]);
}
tmp.erase(it);
break;
} else {
++it;
}
}
// 必要ない三角形ができる可能性があるので削除します
tmp.push_back(tmp[0]);
DeleteRedundantPoint(tmp);
// 終点が追加されてしまうので削除
tmp.pop_back();
}
// 最後の3点
out_points.push_back(tmp[0]);
out_points.push_back(tmp[1]);
out_points.push_back(tmp[2]);
}
1つの頂点と隣り合う頂点を選択してこれが切り取れるかを調べています。
同じ方向にあるかどうかは内積の正負を調べることで判定できます。
切り取った結果不要な頂点が生まれる場合があるので整理しています。
切り取った時に基準とした頂点を取り除いて次の三角形を調べていきます。
せっかく始点と終点を同じにしていましたがこの処理においては邪魔になるので削除しています。
ただそのせいで不要頂点の削除をする際に余計な処理が増えてしましました。これに限らず改善の余地はかなりあると思います。
終わり
多角形の計算では様々な前提があって処理負荷もかなりかかると思います。
用途に応じて必要な分だけ参考にしていただければ幸いです。
以上、過去の自分が知りたかったものの紹介でした。