三角関数
三角関数というのは三角形における角と線分の長さの関係を記述する関数ということになりますが
単純なものだけでもゲームオブジェクトの動作に活用できます
個人的によく使うものを紹介します
単位円
三角関数はsin、cosというものが代表的なものと思います
sin、cosとは具体的にどういう値が出てくるのかを考えるとき、私は頭の中で単位円を思い浮かべます
単位円というのは半径が1の円です
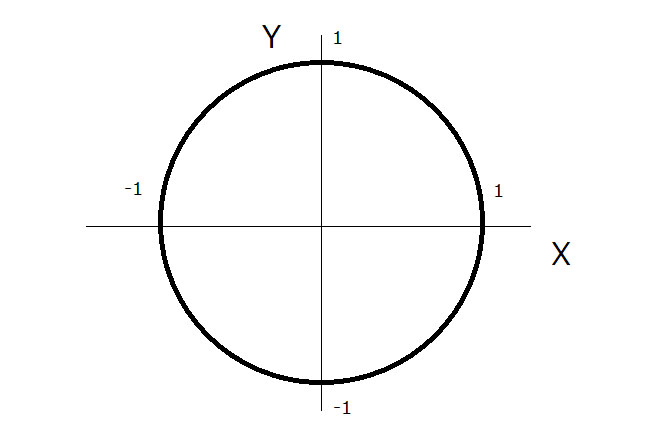
原点から円周上のどこかの点に線を引いたとします
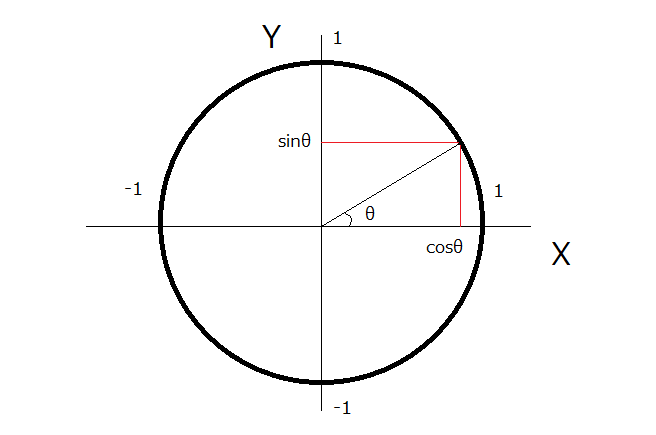
X軸となす角度をθとします
このとき、円周上の点のX値がcosθ、Y値がsinθになります
ベクトルの内積
ここからベクトルとあわせて考えます
ベクトルの計算においてcosθが出てくるものに内積があります
ベクトルA、ベクトルBの内積の結果は以下になりなります
![]()
θというのは2つのベクトルの成す角です
両方のベクトルの長さ1のときはcosθの値そのものになります
先ほどの単位円に当てはめてみます
半径1の円ですのでベクトルの長さは1です
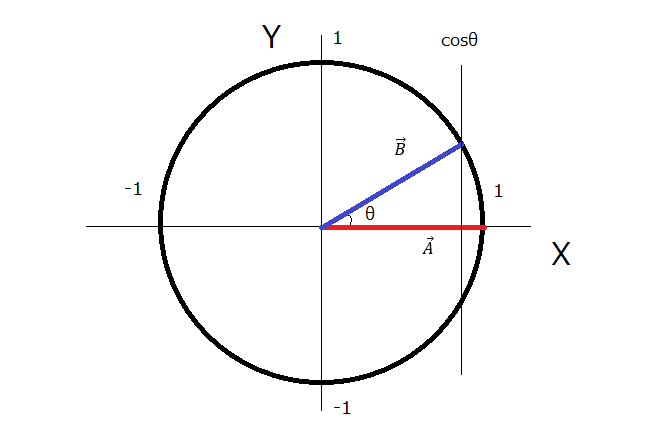
ここから何がわかるかというと
内積値とある角度のcos値を比較することで角度範囲に相手がいるかどうかが判定できます
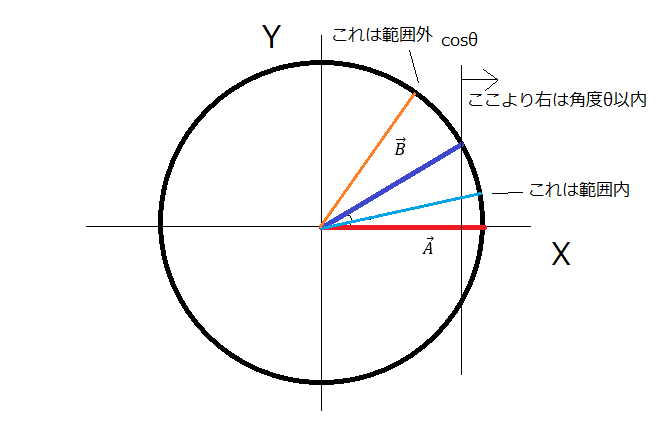
Unityでのプログラムは以下のような感じになります
// 自分の方向
Vector3 a = transform.forward;
// 相手の方向
Vector3 b = new Vector3(0.0f, 0.0f, 1.0f);// 相手の方向の単位ベクトルを設定
// aとbの内積を求める
float dot = Vector3.Dot(a, b);
// cos30°の値を求める。Mathf.Deg2Radはラジアンへの変換
float border = Mathf.Cos(30.0f * Mathf.Deg2Rad);
if (dot > border)
{
// aからみてbの方向が30度以内にいる
}
ベクトルの外積
内積の次は外積です
3次元ベクトルの外積は2つのベクトルに直交するベクトルになります
内積は数値でしたが外積はベクトルです
では直交するベクトルがわかると何なのかですが
ベクトルAをベクトルBに向けるための回転軸に使えます
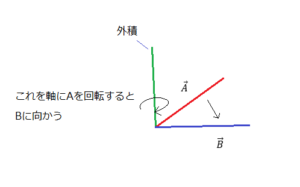
AをBに向けて回転させるわけですがその角度を細かくすることができるのです
相手の方向に段階的に向くという動作が実現できます
例えば秒間30°で回転させるには以下になります
var crossVector = Vector3.Cross(a, b); float rotateAngle = 30.0f * Mathf.Deg2Rad * Time.deltaTime; transform.Rotate(crossVector, rotateAngle);
まとめ
- 内積はcosの値を得ることができます
- cosの値から相手との位置関係が把握できます
- 外積は2つのベクトルに直交するベクトルになります
- 外積の結果を軸に回転することでオブジェクトの向きの制御を容易にできると思います