こんにちは。プログラマの古矢です。
今回はアルゴリズムの話です。
一般化されたアルゴリズムは、検索すればたくさん見つかります。
この記事では一般化されたものではなく、要求に特化したアルゴリズムを取り扱いたいと思います。
要求に特化するとは
一般化されたアルゴリズムは平均的に高性能だったり、相性の悪いデータでも一定の性能を出すようになっていたりします。
しかし、実際のプログラムでは上記のような万能性を要求されないことがあります。例えば、
- 入力データはソートされている
- 入力データに偏りがある
などの場合です。このような場合、万能性を捨てて要求に特化することで、より高性能な動作ができることがあります。
過去に行った特化の例
以前、次のような問題のアルゴリズムを実装しました。
- 扱うデータは「点」と、点同士をつなげる「線」
- 入力は「始点」と「終点」
- 求める答えは、始点から終点へ向かう最短経路上の「最初に訪れる点」
どのような用途かわかるでしょうか。
マップ上に表示する道案内で用いた問題です。
一般化されたアルゴリズムを使うなら、最短経路問題のアルゴリズムを使えば解けるでしょう。
しかし、このとき要求される答えにはいくつかの特徴があり、特化する余地がありました。
特徴1:求める答えが限定されていた
最短経路問題のアルゴリズムはスタートからゴールまでの経路を求めるアルゴリズムです。
しかし、この例で要求される答えは「最初に訪れる点」です。
つまり、終点へ近づく次の点がわかれば、経路まで求める必要はありません。
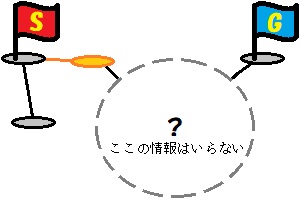
特徴2:閉路がほとんどなかった
閉路とは、簡単に言うと輪っか状の経路です。
これがある場合、スタートからゴールへの経路が複数存在する可能性があります。
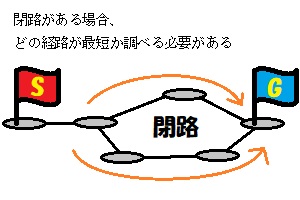
このアルゴリズムを実装した時のデータは偏っていて、この閉路がほとんど存在しませんでした。
そのため、一部の閉路になる個所を除いて、複数経路の可能性を考える必要がありませんでした。
要求に特化する方針
この問題はそもそも、「始点」と「終点」から「最初に訪れる点」が出せる完全なデータベースがあれば、答えは直ちに求まります。
その通りに作れないのは、データ量が膨大になってしまうからです。
データ量と処理速度はトレードオフの関係にあります。
全て計算では処理が重く、全てデータベースではデータ量が膨大です。
今回は要求される答えの特徴を利用して、小さなデータベースを用いて高速に処理することを目指します。
データベースを小さくする
まず、隣の点が1つしかない点は答えが自明です。
なのでデータベースに登録しないことにします。
次に、データベースに載せる点を半分以下にします。
…突然半分以下になりました。
なぜこれほど減らせるかというと、上の2つの特徴に起因します。
特徴1の前提から、始点の1つ隣の点を調べたとき、終点に近づいているとわかれば、それが「最初に訪れる点」として決まります。
特徴2の前提から、始点の1つ隣の点を調べたとき、調べた点から終点へ向かう「最初に訪れる点」が始点を指していなければ、調べた点が「最初に訪れる点」であったことがわかります。
まとめると、次のように調べることができます。
- 隣の点を1つ選ぶ
- 選んだ点から終点へ向かう「最初に訪れる点」を確認
- 2の結果が始点だった場合、終点から遠のいたことになるので、1に戻って他の点を調べる
- 2の結果が始点でなかった場合、終点に近づいたことになるので、これが「最初に訪れる点」である
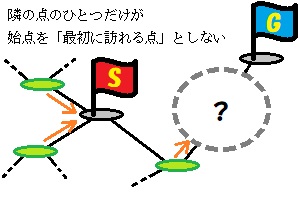
これを実現するために必要なデータベースについて考えます。
全ての点について、以下のことが言えます。
- 自分がデータベースに登録されていなければ、隣の点は全てデータベースに登録されている
- 自分がデータベースに登録されていれば、隣の点は全てデータベースに登録されていない
ひとつの点をデータベースに登録するかしないか決めると、他の全ての点についてもデータベースに登録するかしないかが決まります。
つまり、全ての点は2つのグループに振り分けることができます。
データベースには数が少ないグループを登録します。
これでデータベースに載せる点が半分以下になります。
ここまで残った点を「代表点」としてデータベースを作成します。
特化した結果
他のいくつかの細工と合わせ、特化によって小さなデータベースで高速な処理が実現できました。
ただ、特化すると性能向上できる一方で柔軟性が失われるので、
仕様変更が予感されるときは気を付けましょう。